Granular Rheology
- Kranz, W. T., F. Frahsa, A. Zippelius, M. Fuchs, M. Sperl, PRL 121, 148002 (2018)
- Kranz, W. T., F. Frahsa, A. Zippelius, M. Fuchs, M. Sperl, arXiv:1710.04475
- Kranz, W. T., M. Sperl, EPJ Web Conf 140, 03064 (2017)
That the rheology of granular fluids is special has been realized more than half a century ago by Bagnold.1) In fact, a granular fluid agitated by shear alone displays a non-Newtonian relation, $\sigma = B{\dot\gamma}^2$, between shear stress $\sigma$ and shear rate $\dot\gamma$, different from the linear, Newtonian relation $\sigma = \eta\dot\gamma$, observed in most molecular fluids. Instead of a constant viscosity $\eta$, the Bagnold coefficient $B$ characterizes the granular fluid. In terms of a shear rate dependent viscosity $\eta(\dot\gamma) = B\dot\gamma$, the granular fluid is shear thickening in the Bagnold regime.
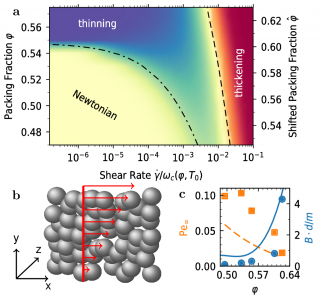 a Rheological state diagram delineating the rheological regimes a indicated in the planne spanned by volume fraction $\varphi$ and shear rate $\dot\gamma$. The dashed line indicates the onset of shear heating and the dash-dotted line indicates the location of $\dot\gamma\tau_{\alpha} = 1$. b Sketch of the linear shear profile. c A comparison of Granular ITT (lines) with Bagnolds measurements (points) regarding the Bagnold coefficient and the associated Peclet number Pe.
a Rheological state diagram delineating the rheological regimes a indicated in the planne spanned by volume fraction $\varphi$ and shear rate $\dot\gamma$. The dashed line indicates the onset of shear heating and the dash-dotted line indicates the location of $\dot\gamma\tau_{\alpha} = 1$. b Sketch of the linear shear profile. c A comparison of Granular ITT (lines) with Bagnolds measurements (points) regarding the Bagnold coefficient and the associated Peclet number Pe.
We studied the shear response of a granular fluid that is kept at a finite granular temperature $T_0$ even with out shear by a homogeneous driving force. In this context we find a rich rheology that comprises, besides the shear thickening Bagnold regime, also a shear thinning and, indeed, a Newtonian regime. The layout of these regimes can be understood qualitatively from a few simple arguments. At high shear rates, we may immediately forget about the homogeneous driving force as shear heating, $\sigma\dot\gamma$, is the dominant energy input. In the stationary state it will be balanced by the dissipation, $n\Gamma\omega_c(T)T$, incurred by the inelastic collisions which occur with a collision frequency $\omega_c(T)$. Here $n$ is the number density of particles and $\Gamma\propto 1-\varepsilon^2$ is the dimensionless cooling rate, related to the coefficient of restitution $\varepsilon$. A non-dimensional shear stress can be defined as $\hat\sigma = \sigma/nT$ such that the power balance, $\sigma\dot\gamma = n\Gamma\omega_c(T)T$ entails $\hat\sigma\dot\gamma = \Gamma\omega_c$, i.e., the collision frequency is proportional to the shear rate. For dimensional reasons $\omega_c(T) \propto\sqrt T$ such that $\sigma \propto T\propto {\dot\gamma}^2$, Bagnold scaling. This breaks down at low density and shear rate, when shear heating is negligible and the temperature is independent of the shear rate. Here we expect Newtonian behaviour. At higher densities, the shear rate may easily exceed the structural relaxation rate $\tau_{\alpha}^{-1}$ of the fluid. In this case, which is particularly pertinent above the Granular Glass Transition, the granular fluid responds like a yield stress fluid with a yield stress $\sigma_y$ that is almost independent of the shear rate. In consequence, the viscosity, $\eta(\dot\gamma) = \sigma_y\dot\gamma$, is decreasing with an increasing shear rate: shear thinning.
All these phenomenological considerations can be made quantitative by extending the Integration Through Transients (ITT) formalism from colloids to granular fluids.