The Granular Glass Transition
- Kranz, W. T., M. Sperl and A. Zippelius, PRL 104, 225701 (2010)
- Sperl, M., W. T. Kranz and A. Zippelius, EPL 98, 28001 (2012)
- Kranz, W. T., M. Sperl and A. Zippelius, PRE 87, 022207 (2013)
Studying an air-fluidized,quasi two dimensional assembly of steel balls, Abate & Durian 1) found that upon increasing the packing fraction $\varphi$, the mean squared displacement $\delta r^2(t) = \langle[r(t+\tau)-r(\tau)]^2\rangle$ develops a plateau for intermediate times. Such a behavior has been observed before in colloidal suspensions and is attributed to a structural glass transition 2).
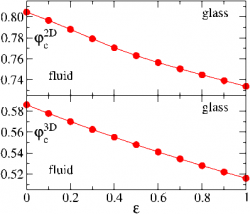 The critical packing fraction $\varphi_c$ as a function of the coefficient of restitution $\varepsilon$ in both two and three dimensions
The critical packing fraction $\varphi_c$ as a function of the coefficient of restitution $\varepsilon$ in both two and three dimensions
Mode coupling theory (MCT) turned out to be successful in describing many features of the (colloidal) glass transition.3) In our work we found that MCT can be generalized to the far from equilibrium stationary state of a model system for fluidized granular particles. We modeled the granular particles as monodisperse smooth spheres with a constant coefficient of restitution $\varepsilon$ and the fluidization by a random force. The central quantity of MCT is the coherent scattering function $\phi(q,t)$ which is given (also for the granular fluid) as the solution of the following equation of motion $$ \ddot\phi(q,t) +\nu_q\dot\phi(q,t) + \Omega^2_q\phi(q,t) +\int_0^td\tau m(q,t-\tau)\dot\phi(q,\tau) = 0. $$ Here, $\nu_q$ and $\Omega_q$, are relaxation frequencies that we calculated explicitly. The memory kernel $m(q,t)$ can be given in terms of a mode coupling approximation $$ m(q,t)\approx \int d^Dk\mathcal V_{\vec q\vec k}\mathcal W_{\vec q\vec k}\phi(q,t)\phi(|\vec q-\vec k|, t). $$ The two vertices or transition rates $\mathcal V_{\vec q\vec k}\ne\mathcal W_{\vec q\vec k}=\frac{1+\varepsilon}{2}\mathcal V_{\vec q\vec k}$ are unequal, different form the theory for colloidal suspensions which are in thermal equilibrium. This difference reflects the loss of detailed balance in the nonequilibrium granular fluid. The inelastic collisions make the direction of time obvious.
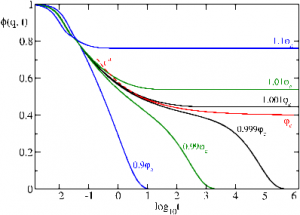 The coherent scattering function $\phi(q,t)$ as a function of time for wave number $qd = 4.2$, coefficient of restitution $\varepsilon=0.7$ and several packing fractions $\varphi$ close to the glass transition.
The coherent scattering function $\phi(q,t)$ as a function of time for wave number $qd = 4.2$, coefficient of restitution $\varepsilon=0.7$ and several packing fractions $\varphi$ close to the glass transition.
As a result we find that there is a glass transition for our driven granular model fluid for all values of the coefficient of restitution and that the MSD indeed develops a plateau