Rough Spheres
- Brilliantov, N. V., Th. Pöschel, W. T. Kranz and A. Zippelius, PRL 98, 28001 (2007)
- Kranz, W. T., N. V. Brilliantov, Th. Pöschel and A. Zippelius, EPJ ST 179, 91 (2009)
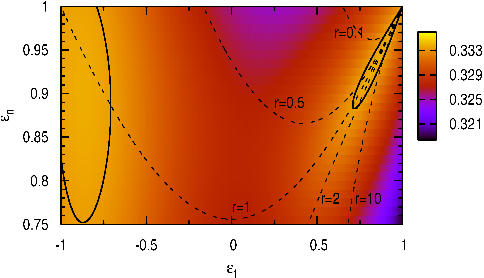Color coded value of the correlation $K$ as a function of the coefficients of restitution $\varepsilon_n,\varepsilon_t$. The solid black lines indicate the lines of vanishing correlations.
The most simple way to model frictional spheres is to introduce a coefficient of tangential restitution $\varepsilon_n$ in addition to the coefficient of normal restitution $\varepsilon_n$. Similar to the case of polydisperse mixtures of granular particles, there is also no equipartition between the translational and rotational degrees of freedom, i.e., the translational temperature $T_{tr}$ is different from the rotational temperature $T_{rot}$. Nevertheless, they attain a fixed ratio $r = T_{rot}/T_{tr}$. 1)
In addition, we found that the spin axis, $\hat\omega$, and the direction of flight, $\hat v$, are correlated. We set up a theory to predict the quantity $K = \langle\cos^2\Theta\rangle$ where $\Theta$ is the angle between $\hat\omega$ and $\hat v$. In case of no correlations one would find $K=1/3$ whereas values $K>1/3$ imply a preference for perpendicular alignment and values $K < 1/3$ a preference for parallel alignment. Depending on the coefficients of restitution all cases are realized. We confirmed this result by event driven simulations.