Trail-Mediated Microbial Interactions
- Kranz, W. T., A. Gelimson, K. Zhao, G. C. L. Wong and R. Golestanian, PRL 117, 038101 (2016)
- Gelimson, A., K. Zhao, C. K. Lee, W. T. Kranz, G. C. L. Wong and R. Golestanian, PRL 117, 178102 (2016)
- Kranz, W. T., R. Golestanian, JCP 150, 214111 (2019)
Pseudomonas aeruginosa leave sticky Psl trails on surfaces they crawl on. A simple model assumes that they are moving along their body orientation, $\hat n = (\cos\varphi, \sin\varphi)$, with a typical speed, $v$, i.e. $$
\dot r(t) = v\hat n(t)
$$ Assuming their propulsion force is a function of the trail concentration, $\psi$, a mechanical model predicts that the bacteria prefer to orient parallel to gradients in the trail concentration. Allowing for some additional orientational diffusion $D_r^0$, the equation of motion for the orientation reads $$
\dot\varphi(t) = \chi\partial_{\perp}\psi(r(t), t) + \xi(t)
$$ where $\chi$ parametrizes the sensitivity to the trail and $\xi$ is the orientational noise.
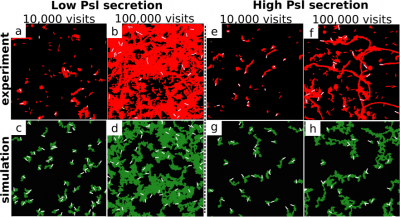
Numerical solutions of a slightly more complicated model reproduce the experimental trail patterns quite nicely (see figure to the right). Concentrating on self-interaction of a bacterium with its own trail on may simplify the trail field $\partial_{\perp}\psi(r, t)$ to a scalar quantity $\partial_{\perp}\psi(t)$ describing the gradient at the bacterium's location and following its own equation of motion $$
\partial_{\perp}\psi(t) = \Omega\tau\int_0^1du(1 - u)[\partial_{\perp}\psi(t-u) + \xi(t-u)/\chi]
$$
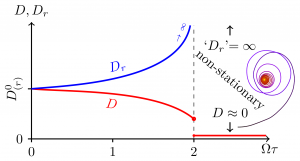 Schematic evolution of the orientational and translational diffusivities with the control parameter $\Omega\tau$ and a typical trajectory in the localized phase. Note the discontinuous jump of $D$ at the transition.
Schematic evolution of the orientational and translational diffusivities with the control parameter $\Omega\tau$ and a typical trajectory in the localized phase. Note the discontinuous jump of $D$ at the transition.
A stochastic delay differential equation parametrized by an effective turning rate $\Omega\tau\propto\chi$. Surprisingly this equation can be solved for $\Omega\tau<2$ yielding an explicit expression for the effective orientational diffusivity $$
D_r/D_r^0 = 1 + \frac{\Omega\tau}{2}\times\frac{1 + \Omega\tau/2}{(1 - \Omega\tau/2)^2}
$$ The self-interactions destabilize the bacterium's orientation reducing its translational diffusivity, $D$, until at the critical value $\Omega\tau=2$ it becomes localized and the diffusivity jumps to essentially zero.